Statistics & Regression

State all assumptions, show all calculations.

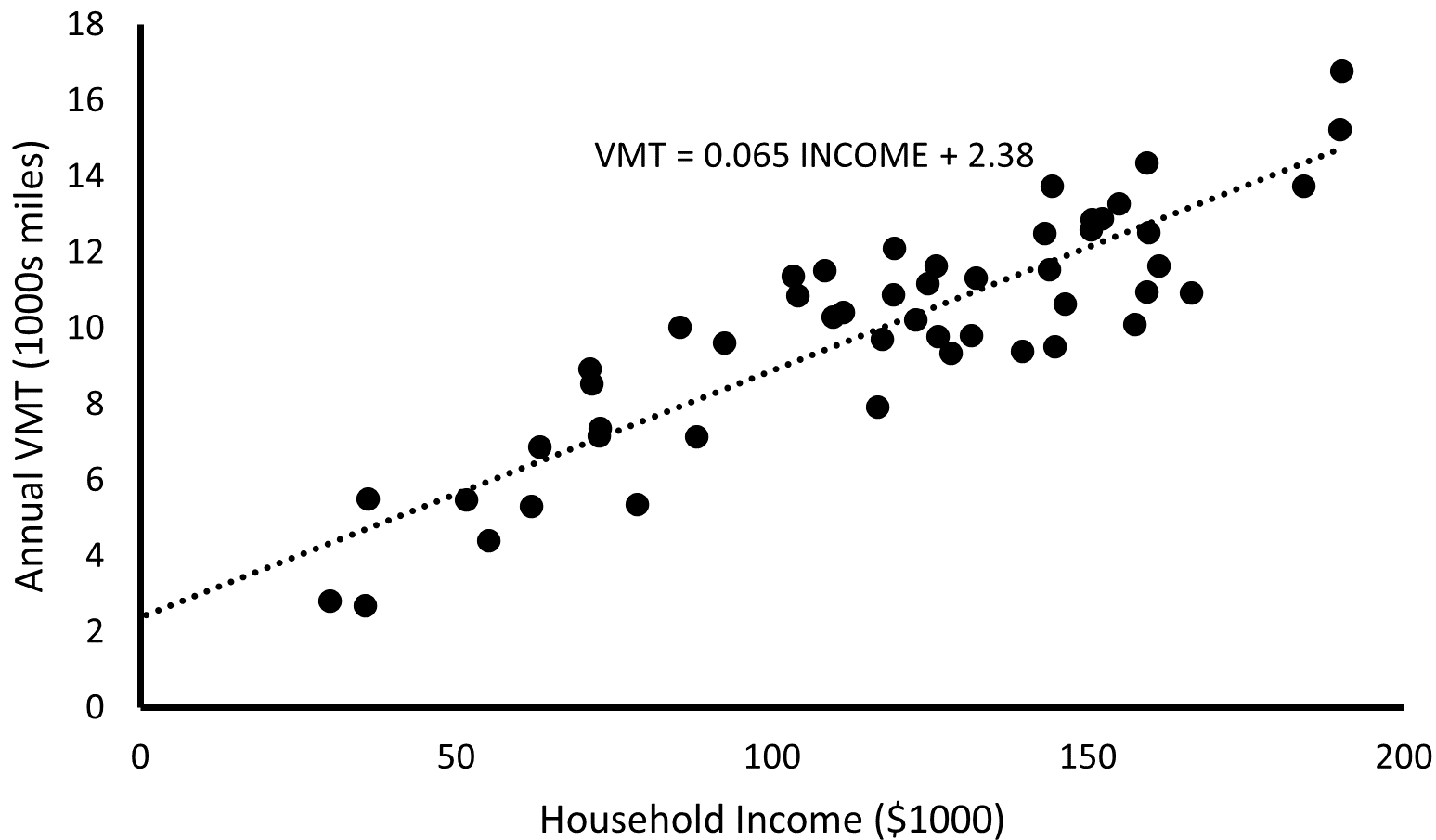
  1. The below figure shows data corresponding to the fitted line y = 0.065x + 2.38 with residual standard deviation 1.42. The residual standard deviation is a measure of remaining variation not captured by the regression model. The range of income is roughly between $29,000 and $195,000.
  1. Sketch hypothetical data (in pen or pencil) with the same range of x (income) but corresponding to the line y = 0.065x + 1.25 with residual standard deviation 1.42.
  2. Sketch hypothetical data (in a different color than in part a) with the same range of x (income) but corresponding to the line y = 0.065x + 1.25 with residual standard deviation 5.0. Note: negative VMT values are fine for this exercise.

Figure 1. Annual VMT by income ($1000)
  1. Give examples of applied statistics problems of interest to you in which the goals are:
  1. Forecasting/classification
  2. Exploring associations
  3. Extrapolation
  4. Causal inference
  1. A survey is conducted in a certain state regarding support for increasing the gas tax to fund transportation investments. In this survey, a higher tax is supported by 50% of respondents aged 18-29, 60% of respondents aged 30-44, 25% of respondents aged 45-64, and 10% of respondents aged 65 and up. Use the weighted average formula (available in many places online) to compute the proportion of respondents in the sample who support a higher tax. Assume there is no nonresponse.
  1. For the sample: Suppose the sample includes 50 respondents aged 18-29, 300 aged 30-44, 275 aged 45-64, and 375 aged 65+.
  2. For the Nebraska population: Assume the state where the survey was performed is Nebraska. How would you adjust your weighted average to represent the population? Assume the following population distribution for the state.
Table 1. Population Distribution for Nebraska
Age group NE population
18-29 265260
30-44 368768
45-64 458101
65+ 312458
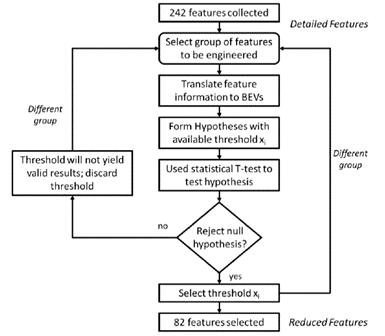
  1. An analyst is interested in the relationship between demographic features and electric vehicle (EV) adoption. They develop a procedure to determine variables that might affect adoption (see figure below). Their procedure starts with 242 features (variables), which they narrow to 82 features using t-test statistics. In the below figure, the term “features to be engineered” simply refers to combining and transforming variables to reduce the number of features and/or their correlation. As a hint, this study was chosen as an example of low-quality analysis. There may be no clear interpretation to a figure, and it is acceptable to state this conclusion.
  1. Please comment on the validity of this procedure. Note: There is no single solution to this problem. The goal is to start thinking about data analysis.

Figure 2. Analysis workflow
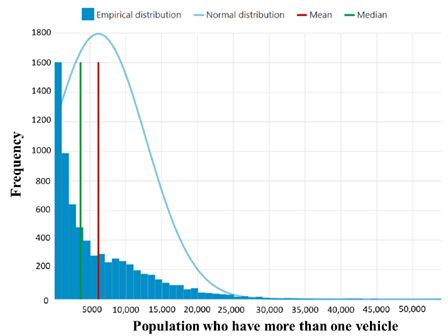
  1. The analyst generates the following figure. What information is provided by this figure? Is its implication evident from the available information? What additional information would help to clarify its interpretation?

Figure 3. Histogram plot showing population with more than one vehicle, illustrating the highly non-normal distribution of a typical demographic feature